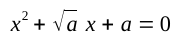Τεκμηριώνεται επιστημονικά η Β’ (και η Α’) ανάθεση του μαθήματος των μαθηματικών σε πληροφορικούς στην β/βάθμια εκπαίδευση;

Ως γνωστόν, με βάση το άρθρο 30 του Ν.2009/1992 (ΦΕΚ 18/14-2-1992, τ.Α ́) “Εθνικό Σύστημα Επαγγελματικής Εκπαίδευσης και Κατάρτισης και άλλες διατάξεις” μετατάχθηκαν στον νεοσύστατο τότε εκπαιδευτικό κλάδο Π19, λόγω έλλειψης απόφοιτων πληροφορικής, εκπαιδευτικοί χωρίς πτυχίο πληροφορικής, κυρίως μαθηματικοί. Θεωρώ ότι δικαιωματικά ένας μαθηματικός είναι η πρώτη επιλογή αναπλήρωσης ενός πληροφορικού όταν προκύψει ανάγκη, θα δείξω, μάλιστα, ότι αυτή η “συνάρτηση” είναι “αντιστρέψιμη”, δηλαδή ότι και ένας πληροφορικός είναι η πρώτη επιλογή αναπλήρωσης ενός μαθηματικού.

–Η σχέση πληροφορικής-μαθηματικών είναι εσωτερική-δομική και όχι εξωτερική-εργαλειακή.

Η εργαλειακή χρήση των μαθηματικών, όπως άλλωστε και της πληροφορικής, λαμβάνει χώρα σε μια πληθώρα επιστημών και ειδικοτήτων. Για παράδειγμα, η επιστήμη της φυσικής χρησιμοποιεί τα μαθηματικά ως εργαλείο με σκοπό την μοντελοποίηση του αντικείμενου της μελέτης της, του φυσικού κόσμου, ο οποίος δεν είναι αυτός καθαυτός αυστηρά ορισμένο μαθηματικό αντικείμενο – τουλάχιστον κανείς μέχρι τώρα δεν έχει καταφέρει να αποδείξει κάτι τέτοιο.

Από την άλλη πλευρά, το θεμελιώδες αντικείμενο της πληροφορικής είναι οι αλγόριθμοι, ευρύτερα γνωστοί ως “προγράμματα”, οι οποίοι είναι ένα αυστηρά ορισμένο μαθηματικό αντικείμενο, αυτοί καθαυτοί. Οι αλγόριθμοι δεν “χρησιμοποιούν τα μαθηματικά”, αλλά χρησιμοποιούν τα…υπόλοιπα μαθηματικά, όπως και τα υπόλοιπα μαθηματικά χρησιμοποιούν τους αλγόριθμους, αν όχι θεμελιώνονται πάνω στους τελευταίους σε κάποιο βαθμό.

Το 1931 ο Γκέντελ δημοσίευσε τα περίφημα θεωρήματα μη-πληρότητας. Η απόδειξή του βασίστηκε πάνω στην επιμέρους απόδειξη ότι οι πρωτόγονες αναδρομικές συναρτήσεις (ένα υποσύνολο των προγραμμάτων) αναπαριστάνονται στην πρωτοβάθμια αριθμητική Peano, με άλλα λόγια είναι αυστηρά ορισμένα μαθηματικά αντικείμενα σε μια τόσο θεμελιώδη μαθηματική θεωρία όπως η αριθμητική. Αυτό αποδεικνύεται και για το σύνολο των προγραμμάτων (μ-Αναδρομικές συναρτήσεις). Για την αναπαράσταση αυτή, μάλιστα, δεν είναι αναγκαίο καν το αξιωματικό σχήμα της επαγωγής, αρκούν οι δύο γνωστές πράξεις, της πρόσθεσης και του πολλαπλασιασμού!

-Οι αλγόριθμοι είναι θεμέλιο των μαθηματικών.

Συνεπάγεται από την προηγούμενη διαπίστωση. Εφόσον οι αλγόριθμοι είναι κομμάτι της πρωτοβάθμιας αριθμητικής Peano, η οποία για ευνόητους λόγους θεωρείται θεμέλιο των μαθηματικών, τότε και οι ίδιοι συνιστούν θεμελιώδες συστατικό των μαθηματικών.

-Τα θεμέλια συναντούν πολύ συχνά τα άλλα θεμέλια (προτασιακό και κατηγορηματικό λογισμό).

Τα τμήματα της τριτοβάθμιας εκπαίδευσης τα οποία χρησιμοποιούν εργαλειακά τα μαθηματικά, συνήθως περιλαμβάνουν στο πρόγραμμα σπουδών τους μια σειρά μαθημάτων των μαθηματικών κλάδων της ανάλυσης και (σπανιότερα) της γραμμικής άλγεβρας, αλλά όχι θεμέλια των μαθηματικών όπως ο προτασιακός και κατηγορηματικός λογισμός. Αυτά τα αντικείμενα αποτελούν στην πλειονότητα των περιπτώσεων αναπόσπαστο κομμάτι των προγραμμάτων σπουδών των διαφόρων τμημάτων πληροφορικής (τα οποία συνιστούν τους εκπαιδευτικούς κλάδους Π19 και Π20) και θέτουν τις βάσεις για μια βαθιά κατανόηση των μαθηματικών η οποία είναι πάνω από κάθε σύγκριση με την όποια εξωτερική-εργαλειακή τους χρήση.

–Η μελέτη των αλγορίθμων απαιτεί ένα ακόμα ευρύτερο μαθηματικό υπόβαθρο, γεγονός το οποίο επιβεβαιώνουν τα προγράμματα σπουδών της πλειονότητας των τμημάτων πληροφορικής.

Πέρα από τον προτασιακό και κατηγορηματικό λογισμό, συνήθη μαθηματικά αντικείμενα ή μοντέρνες φαρμογές των μαθηματικών στα προγράμματα σπουδών πληροφορικής είναι:

• Aνάλυση
• Γραμμική άλγεβρα
• Θεωρία πιθανοτήτων
• Θεωρία συνόλων
• Συνδυαστική
• Θεωρία των γράφων
• Θεωρία υπολογισιμότητας
• Θεωρία αυτομάτων και τυπικών γλωσσών
• Θεωρία πολυπλοκότητας
• Θεωρία πληροφορίας
• Κρυπτογραφία
• Γραμμικός προγραμματισμός
• Άλγεβρα Μπουλ
• Θεωρία παιγνίων
• …
• …
• …

-Οι αλγόριθμοι είναι παντού στα μαθηματικά.

Ξεκινώντας την μαθηματική εκπαίδευση ήδη από τις πρώτες τάξης του Δημοτικού και συνεχίζοντας σε υψηλότερες βαθμίδες της εκπαίδευσης, διδάσκονται:

• Ο αλγόριθμος της προπαίδειας.
• Ο αλγόριθμος της κάθετης πρόσθεσης και αφαίρεσης.
• Ο αλγόριθμος του κάθετου πολλαπλασιασμού και της κάθετης διαίρεσης.
• Αλγόριθμοι εύρεσης του ελάχιστου κοινού πολλαπλασίου (ΕΚΠ).
• Αλγόριθμοι εύρεσης του μέγιστου κοινού διαιρέτη (ΜΚΔ.)
• Αλγόριθμοι για την μετατροπή δύο κλασμάτων σε ομώνυμα.
• Αλγόριθμοι πρόσθεσης κλασμάτων.
• Ο αλγόριθμος «το κόσκινο του Ερατοσθένη».
• Ο αλγόριθμος κατασκευής ισοσκελούς τριγώνου με χάρακα και διαβήτη.
• Ο αλγόριθμος διχοτόμησης ευθύγραμμου τμήματος με χάρακα και διαβήτη.
• Ο αλγόριθμος διχοτόμησης γωνίας με χάρακα και διαβήτη.
• Ο αλγόριθμος υπολογισμού ρητής προσέγγισης τετραγωνικής ρίζας φυσικού αριθμού.
• Ο αλγόριθμος επίλυσης (στο ℝ) μονομεταβλητής πρωτοβάθμιας εξίσωσης με ρητούς συντελεστές.
• Ο αλγόριθμος επίλυσης (στο ℝ) μονομεταβλητής δευτεροβάθμιας εξίσωσης με ρητούς συντελεστές.
• Αλγόριθμοι παραγώγισης για διάφορες κλάσεις συναρτήσεων.
• Αλγόριθμοι ολοκλήρωσης για διάφορες κλάσεις συναρτήσεων.
• …
• …
• …

–Οι αλγόριθμοι οριοθετούν τα μαθηματικά.

Η οριοθέτηση μιας επιστήμης είναι απαραίτητη, χρήσιμη, και προσδίδει κύρος σ’ αυτήν. Συνεισφέρει στo να μην καταβάλλεται μάταιη προσπάθεια σε ανέφικτους στόχους. Αν το θεώρημα Lindemann–Weierstrass από το οποίο συνεπάγεται ότι δεν είναι δυνατός ο τετραγωνισμός του κύκλου αποδεικνυόταν νωρίτερα από το 1882, αυτό το πρόβλημα θα απασχολούσε την επιστήμη των μαθηματικών για λιγότερο χρόνο από όσο τελικά την απασχόλησε. Έτσι, τα θεωρήματα μη-πληρότητας του Γκέντελ, η απόδειξη των οποίων όπως είδαμε θεμελιώνεται πάνω στους αλγόριθμους, συνεισφέρουν, για παράδειγμα, στο να μην ασχολούνται οι μαθηματικοί με την απόδειξη της συνέπειας της συνολοθεωρίας ZFC εντός του ZFC, εκτός κι αν θέλουν να αποδείξουν ότι το ZFC είναι ασυνεπές.

Οι αλγόριθμοι όμως δεν οριοθετούν τα μαθηματικά μόνο μέσω των θεωρημάτων μη-πληρότητας του Γκέντελ, αλλά και πιο άμεσα, μέσω του θεωρήματος του τερματισμού του “πατέρα της πληροφορικής”, Άλαν Τούρινγκ. Το πρόβλημα του τερματισμού, το οποίο ο Τούρινγκ απέδειξε ότι είναι “μη-αποφασίσιμο, “ανάγεται” σε διάφορα γνωστά προβλήματα στα μαθηματικά, τα οποία, ως συνέπεια, αποδεικνύονται και αυτά “μη-αποφασίσιμα”. Για παράδειγμα, γνωρίζουμε ότι δεν υπάρχει αλγόριθμος ο οποίος επιλύει στο ℝ κάθε δευτεροβάθμια εξίσωση με πραγματικούς συντελεστές. Επίσης, ότι δεν υπάρχει αλγόριθμος για το πρόβλημα της ισότητας δύο πραγματικών αριθμών, καθώς και για πληθώρα άλλων προβλημάτων.

Η ύπαρξη αλγορίθμων είναι τόσο σημαντική για τα μαθηματικά, όσο και η ανυπαρξία τους!

-Όλα (σχεδόν) τα μαθηματικά μέσα σ’ έναν αλγόριθμο.

Η συνολοθεωρία ZFC αποτελεί δικαιολογημένα θεμέλιο των μαθηματικών, αφού μέχρι τώρα σχεδόν όλα (πλην ελάχιστων εξαιρέσεων) τα μαθηματικά θεωρήματα, αποδεικνύονται μέσα σ΄ αυτήν. Και επειδή πρόκειται για μια “πρωτοβάθμια” θεωρία, το πρόβλημα της “k-αποδειξιμότητας” (k-provability problem) γι’ αυτήν είναι αποφασίσιμο.

Με απλά λόγια αυτό μας λέει ότι δεδομένου ενός ισχυρισμού ο οποίος μπορεί να διατυπωθεί μέσα στην ZFC, υπάρχει αλγόριθμος ο οποίος απαντάει σωστά “ναι” ή “όχι” στο ακόλουθο ερώτημα:

υπάρχει απόδειξη στην ZFC για τον δεδομένο ισχυρισμό της οποίας το μέγεθος είναι το πολύ k σύμβολα; (μια απόδειξη είναι τυπικά μια συμβολοσειρά).

-Ένα από τα μεγαλύτερα ανοιχτά προβλήματα των μαθηματικών σήμερα (αν όχι το μεγαλύτερο) είναι ένα πρόβλημα πληροφορικής: το πρόβλημα P versus NP.

Το ινστιτούτο μαθηματικών Clay έχει ανακηρύξει επτά μαθηματικά βραβεία για την επίλυση αντίστοιχων επτά μαθηματικών προβλημάτων, γνωστών ως Millenium Problems (Προβλήματα της Χιλιετίας). Κάθε βραβείο συνοδεύεται από το χρηματικό ποσό του ενός εκατομμυρίου δολαρίων. Ένα από τα προβλήματα αυτά είναι το P versus NP, το οποίο μπορεί να διατυπωθεί στην ακόλουθη (σχετικά απλοποιημένη) μορφή:

Ο καλύτερος αλγόριθμος μέχρι τώρα για την επίλυση του προβλήματος της k-αποδειξιμότητας της θεωρίας ZFC (το οποίο διατυπώθηκε παραπάνω) είναι αρκετά αργός (“εκθετικός”) για να είναι χρήσιμος-αποδοτικός. Υπάρχει ένας αρκετά γρήγορος (“πολυωνυμικός”) αλγόριθμος, ώστε να είναι χρήσιμος-αποδοτικός;

Επίλογος

Τεκμηριώνεται, λοιπόν, επιστημονικά η Β’ (και η Α’) ανάθεση του μαθήματος των μαθηματικών σε πληροφορικούς στην δευτεροβάθμια εκπαίδευση; Τα συμπεράσματα δικά σας.

Μια δευτεροβάθμια εξίσωση με πραγματικούς συντελεστές η οποία είναι αδύνατο να επιλυθεί στο ℝ

τελευταία αναθεώρηση 4/3/2017, 23:00

Όπως έχω αποδείξει στην εργασία μου (2016), δεν υπάρχει γενική μέθοδος για την επίλυση της δευτεροβάθμιας εξίσωσης με πραγματικούς συντελεστές στο ℝ. Αυτό, βέβαια, δεν σημαίνει απαραίτητα ότι δεν ισχύει ότι κάθε δευτεροβάθμια εξίσωση με πραγματικούς συντελεστές μπορεί να επιλυθεί στο ℝ από μια ειδική (ανά εξίσωση) μέθοδο. Ωστόσο, θα αποδείξω παρακάτω το πιο ισχυρό αποτέλεσμα (-τουλάχιστον στα συνήθη μαθηματικά), ότι δηλαδή μία συγκεκριμένη δευτεροβάθμια εξίσωση με πραγματικούς συντελεστές δεν είναι δυνατό να επιλυθεί στο ℝ (ούτε από μια ειδική μέθοδο) με την προϋπόθεση βέβαια ότι τα συνήθη μαθηματικά έχουν κάποια γνωστή αξία. Όταν μιλάμε για “συνήθη μαθηματικά” εννοούμε το αξιωματικό σύστημα της θεωρίας των συνόλων ZFC, μιας και δεν υπάρχει κάποια συνήθης μαθηματική θεωρία η οποία δεν μπορεί να προσομοιωθεί από το ZFC – γι’ άλλωστε και το ZFC θεωρείται “θεμέλιο” και η πιο γενική μορφή των μαθηματικών. Όταν λέμε ότι “τα συνήθη μαθηματικά έχουν κάποια γνωστή αξία” εννοούμε ότι είναι συνεπή, δηλαδή δεν αποδεικνύουν κάποιον ισχυρισμό και την άρνησή του, δηλαδή μια αντίφαση. Ένα μαθηματικό σύστημα το οποίο αποδεικνύει μια αντίφαση έχει αποδειχτεί ότι μπορεί να αποδείξει οποιονδήποτε ισχυρισμό, κάτι που είναι γνωστό ως “αρχή της έκρηξης”. Ένα τέτοιο σύστημα δεν έχει κάποια γνωστή αξία.

Μια μηχανή Turing είναι ένα μαθηματικό αντικείμενο το οποίο εισήγαγε ο “πατέρας” – κατά κοινή ομολογία – της επιστήμης των υπολογιστών Alan Turing λίγο πριν τα μέσα του προηγούμενου αιώνα, και είναι ισοδύναμο με ένα πρόγραμμα σε μια σύγχρονη γλώσσα προγραμματισμού. “Ισοδύναμο” σημαίνει ότι για κάθε μηχανή Turing υπάρχει ένα πρόγραμμα σε Γλώσσα ΑΕΠΠ, c, java ή οποιαδήποτε άλλη σύγχρονη γλώσσα προγραμματισμού, το οποίο εκτελεί τον ίδιο υπολογισμό, αλλά και αντίστροφα για κάθε πρόγραμμα σε μια σύγχρονη γλώσσα προγραμματισμού, υπάρχει μια μηχανή Turing η οποία εκτελεί τον ίδιο υπολογισμό. Η διαφορά τους είναι ότι η μηχανή Turing είναι πιο απλό (και ένα από τα απλούστερα) υπολογιστικό μοντέλο, με την έννοια ότι η γενική περιγραφή της λειτουργίας μιας μηχανής Turing είναι σχετικά (πολύ) πιο σύντομη. Κάτι τέτοιο ευνοεί φυσικά την μελέτη των ιδιοτήτων του υπολογισμού.

Μια μηχανή Turing εκτελεί έναν υπολογισμό σε διακριτά βήματα, κάτι που σε ένα σύγχρονο προγραμματιστικό περιβάλλον προσομοιάζει με την εκτέλεση ενός προγράμματος βήμα-βήμα στον debugger. Μια άλλη βασική ιδιότητα της μηχανής Turing είναι ότι τερματίζει ή δεν τερματίζει (“κολλάει”). Ισοδύναμα ένα πρόγραμμα σε μια σύγχρονη γλώσσα προγραμματισμού λέμε ότι πέφτει σε “ατέρμονα βρόγχο”, δηλαδή δεν τερματίζει ή κολλάει, ενώ τερματίζει αν δεν πέφτει σε ατέρμονα βρόγχο. Σε κάθε διακριτό βήμα της λειτουργίας της μηχανής Turing μπορεί να αποφασισθεί αν η μηχανή τερματίζει ή όχι (στο συγκεκριμένο βήμα), ενώ το γενικότερο πρόβλημα, δηλαδή αν μια (οποιαδήποτε) μηχανή Turing τερματίζει (σε κάποιο βήμα) ή δεν τερματίζει σε κανένα βήμα έχει αποδειχτεί ότι δεν επιλύεται (τουλάχιστον από μια μηχανή Turing – θα πρέπει να σημειωθεί εδώ ότι η μηχανή Turing – ή ισοδύναμα οποιαδήποτε σύγχρονη γλώσσα προγραμματισμού – είναι το ισχυρότερο υπολογιστικό μοντέλο που έχει ανακαλύψει ο άνθρωπος μέχρι τώρα, με άλλα λόγια σε 4.000 περίπου χρόνια μαθηματικής ιστορίας κανείς δεν έχει παρουσιάσει κάποιον υπολογισμό με χαρτί και μολύβι ή με οποιοδήποτε άλλο μέσο, ο οποίος να μην μπορεί να προσομοιωθεί από μια μηχανή Turing. Η υπόθεση ότι ένα ισχυρότερο από την μηχανή Turing υπολογιστικό μοντέλο δεν υπάρχει, είναι γνωστή ως “θέση Church-Turing”).

Οι Yedidia & Aaronson (2016) κατασκεύασαν την μηχανή Turing Ζ η οποία δεν τερματίζει αν και μόνο αν το ZFC είναι συνεπές, ή ισοδύναμα τερματίζει αν και μόνο αν το ZFC δεν είναι συνεπές. Θεωρείστε τον πραγματικό αριθμό α ο οποίος ορίζεται ως εξής:

Ακέραιο μέρος της δεκαδικής αναπαράστασής του ίσο με το 0 και το νιοστό ψηφίο της δίνεται από την συνάρτηση f(ν), για ν θετικό ακέραιο:

Είναι προφανές ότι:

α = 0 αν και μόνο αν η μηχανή Turing Z δεν τερματίζει (ποτέ)

Ή ισοδύναμα:

α = 0 αν και μόνο αν το ZFC είναι συνεπές (1)

Ή ισοδύναμα:

α ≠ 0 αν και μόνο αν το ZFC είναι ασυνεπές (2)

Θεωρείστε τώρα την ακόλουθη δευτεροβάθμια εξίσωση:

Η διακρίνουσα του τριωνύμου είναι:

Αν κάποιος, λοιπόν, αποδείξει με τα συνήθη μαθηματικά ότι η παραπάνω εξίσωση δεν έχει λύσεις στο ℝ, συνεπάγεται:

Οπότε, από την (2) παίρνουμε ότι το ZFC είναι ασυνεπές, δηλαδή τα συνήθη μαθηματικά είναι άχρηστα.

Αν πάλι αποδείξει με τα συνήθη μαθηματικά ότι η παραπάνω εξίσωση έχει λύσεις στο ℝ, συνεπάγεται:

Οπότε, από από την (1) παίρνουμε ότι το ZFC είναι αποδεδειγμένα συνεπές από το ίδιο το ZFC. Το ZFC, όμως, προσομοιώνει, βέβαια, και την “πρωτοβάθμια αριθμητική Peano”, οπότε από το δεύτερο θεώρημα μη-πληρότητας του Gödel παίρνουμε ότι το ZFC είναι ασυνεπές (εφόσον αποδεικνύει το ίδιο την συνέπειά του)!

Με άλλα λόγια, οποιαδήποτε απόδειξη στα συνήθη μαθηματικά, είτε περί της ύπαρξης, είτε περί της μη-ύπαρξης λύσεων στο ℝ της παραπάνω εξίσωσης τα καθιστά άχρηστα. Άρα, αν δεν είναι άχρηστα, δεν υπάρχει απόδειξη εντός αυτών ούτε ότι η εξίσωση αυτή έχει λύσεις στο ℝ, ούτε ότι δεν έχει. Δηλαδή, η εξίσωση αυτή είναι αδύνατο να επιλυθεί στο ℝ με τα συνήθη μαθηματικά (αν τα τελευταία είναι συνεπή).

Δεν υπάρχει αλγόριθμος για την επίλυση της δευτεροβάθμιας εξίσωσης με πραγματικούς συντελεστές στο ℝ

Σημείωση: το παρακάτω να μην ληφθεί υπόψη από τους υποψήφιους για το μάθημα της Πληροφορικής στις Πανελλαδικές εξετάσεις. Αυτή η εργασία απαιτεί πληροφορικό και μαθηματικό υπόβαθρο το οποίο δεν καλύπτεται από τα σχολικά βιβλία.

Δεν υπάρχει αλγόριθμος για την επίλυση της δευτεροβάθμιας εξίσωσης με πραγματικούς συντελεστές στο ℝ

Γιώργος Μπουγιούκας, 2016

georgebougioukas@yahoo.com

Περίληψη. Αυτή η εργασία αποδεικνύει ότι το πρόβλημα της ισότητας δύο πραγματικών σταθερών είναι μη-αποφασίσιμο και ως συνέπεια ότι δεν υπάρχει αλγόριθμος για την επίλυση της δευτεροβάθμιας εξίσωσης με πραγματικούς συντελεστές στο ℝ.

1. Ορισμοί-Υποθέσεις

α)  Ένας αλγόριθμος είναι μια μηχανή Turing. Σημειώστε ότι μέχρι αυτή την στιγμή δεν έχει βρεθεί «αλγόριθμος» ο οποίος να επιλύει οποιοδήποτε μαθηματικό πρόβλημα με οποιοδήποτε τρόπο (πχ με χαρτί και μολύβι) και να μην μπορεί να προσομοιωθεί από μια μηχανή Turing ή «ισοδύναμα» από ένα πρόγραμμα σ’ έναν σύγχρονο ηλεκτρονικό υπολογιστή – αν συνέβαινε κάτι τέτοιο, τα μαθηματικά πιθανότατα δεν θα ήταν όπως τα ξέρουμε σήμερα.

β) Υποθέτουμε ότι ένας αλγόριθμος (A1) για την επίλυση της δευτεροβάθμιας εξίσωσης με πραγματικούς συντελεστές στο ℝ δίνει αναγκαστικά ένα αποτέλεσμα το οποίο συνεπάγεται την αποφασισιμότητα του προβλήματος απόφασης “υπάρχει πραγματική λύση για την δοσμένη εξίσωση;” (Π1), για παράδειγμα:

Μια λίστα, κενή αν η δοσμένη εξίσωση δεν έχει καμία πραγματική λύση, με το πολύ δύο στοιχεία (ανά δύο άνισα), διαφορετικά.

2. Απόδειξη

Θα αποδείξουμε το παρακάτω θεώρημα:

Το πρόβλημα της ισότητας δύο πραγματικών σταθερών είναι μη-αποφασίσιμο (Θ1).

Έστω C(TM) η κωδικοποίηση σε συμβολοσειρά μιας μηχανής Turing TM. Για κάθε μηχανή Turing και κάθε συμβολοσειρά εισόδου (επί του αλφάβητου της TM) x, θεωρούμε την σειρά:

Η σειρά αυτή είναι συγκλίνουσα στο ℝ, αφού για k≥1 είναι προφανώς 10^-kh_C(TM),x(k)≤10^-k και η σειρά της ακολουθίας 10^-k είναι συγκλίνουσα, αφού η ακολουθία 10^-k είναι γεωμετρική με λόγο 10^-1  και ισχύει |10^-1| < 1. Επομένως, για κάθε μηχανή Turing TM και συμβολοσειρά εισόδου (επί του αλφάβητου εισόδου της TM) x ισχύει το παρακάτω λήμμα:

Προφανώς,  για κάθε μηχανή Turing TM και κάθε συμβολοσειρά εισόδου (επί του αλφάβητου της TM) x ισχύει και το παρακάτω λήμμα:

Θεωρούμε μια (οποιαδήποτε) μηχανή Turing TM₁ με είσοδο μια (οποιαδήποτε επί του αλφάβητου εισόδου της TM₁) συμβολοσειρά x₁. Υποθέτοντας ότι υπάρχει αλγόριθμος (Α3) ο οποίος αποφασίζει αν δύο πραγματικές σταθερές είναι ίσες, συνεπάγεται ότι υπάρχει ένας άλλος αλγόριθμος (Α4) ο οποίος:

α) Προσομοιώνοντας τον αλγόριθμο Α3 αποφασίζει αν ισχύει ή όχι ότι (το πρώτο μέλος της παρακάτω ισότητας είναι πραγματική σταθερή με βάση το Λ1):

β) Με βάση το προηγούμενο αποτέλεσμα και το Λ2 αποφασίζει αν η μηχανή Turing TM₁ με είσοδο x₁ τερματίζει.

Με άλλα λόγια ο αλγόριθμος Α4 αποφασίζει το πρόβλημα του τερματισμού, αποτέλεσμα το οποίο έρχεται σε αντίφαση με το θεμελιώδες “θεώρημα του τερματισμού” του Alan Turing (Χαλάτσης, 2003, σ. 107). Καταλήξαμε σε αντίφαση γιατί θεωρήσαμε ότι ο αλγόριθμος Α3 υπάρχει. Επομένως, ένας τέτοιος αλγόριθμος δεν υπάρχει. ▪

Αν ο αλγόριθμος Α1 υπάρχει, μέσω της υπόθεσης β) στην ενότητα 1, συνεπάγεται ότι υπάρχει ένας άλλος αλγόριθμος (Α2), ο οποίος, προσομοιώνοντας τον Α1, δοσμένης οποιαδήποτε δευτεροβάθμιας εξίσωσης με πραγματικούς συντελεστές, αποφασίζει το πρόβλημα απόφασης Π1. Αν η μορφή της εξόδου του αλγορίθμου Α1  είναι ταυτόσημη με αυτή του παραδείγματος της υπόθεσης β) στην ενότητα 1, ο αλγόριθμος Α2 αποφασίζει το Π1 ως εξής:

– Αν ο αλγόριθμος Α1 δώσει ως αποτέλεσμα μια μη-κενή λίστα – δηλαδή υπάρχει πραγματική λύση για την δοσμένη εξίσωση – δίνει ως αποτέλεσμα “Αληθές”.

– Αλλιώς, αν ο αλγόριθμος Α1 δώσει ως αποτέλεσμα μια κενή λίστα – δηλαδή δεν υπάρχει πραγματική λύση για την δοσμένη εξίσωση – δίνει ως αποτέλεσμα “Ψευδές”.

Έστω r, s πραγματικές σταθερές και d = |s – r|. Θεωρούμε την ακόλουθη  δευτεροβάθμια εξίσωση με πραγματικούς συντελεστές:

Δοσμένου ενός στιγμιότυπου του Π1 αποτελούμενου από την Ε1, ο αλγόριθμος Α2 δίνει το ακόλουθο αποτέλεσμα:

– Είτε “Αληθές”, που σημαίνει ότι η Ε1 έχει τουλάχιστον μία πραγματική λύση – οπότε αν Δ η διακρίνουσα της Ε1:

– Είτε “Ψευδές”, που σημαίνει ότι η Ε1 δεν έχει πραγματικές λύσεις – οπότε αν Δ η διακρίνουσα της Ε1:

Οι πραγματικές σταθερές s και r δεν έχουν κάποια ιδιαίτερη ιδιότητα. Το ίδιο ισχύει και για τον αλγόριθμο Α2, εκτός από το ότι χρησιμοποιεί το αποτέλεσμα του αλγόριθμου Α1, ο οποίος επίσης δεν έχει κάποια ιδιαίτερη ιδιότητα, εκτός από την υποτιθέμενη μορφή του αποτελέσματος που εξάγει. Επομένως, για κάθε s, r ∈ ℝ μπορεί να κατασκευαστεί η εξίσωση Ε1 και να δοθεί ως είσοδος στον αλγόριθμο Α2, του οποίου το αποτέλεσμα τότε συνεπάγεται ότι είτε s=r είτε s≠r, δηλαδή το πρόβλημα της ισότητας δύο πραγματικών σταθερών είναι αποφασίσιμο, το οποίο έρχεται σε αντίφαση με το Θ1. Καταλήξαμε σε αντίφαση γιατί υποθέσαμε ότι ο αλγόριθμος Α1 υπάρχει. Επομένως, τέτοιος αλγόριθμος δεν υπάρχει. ▪

Βιβλιογραφικές αναφορές

Χαλάτσης Κ. (2003). Θεμελιώσεις Επιστήμης Η/Υ, Τόμος Β’- Θεωρία Υπολογισμού. Πάτρα, Ελληνικό Ανοικτό Πανεπιστήμιο.