τελευταία αναθεώρηση 4/3/2017, 23:00
Όπως έχω αποδείξει στην εργασία μου (2016), δεν υπάρχει γενική μέθοδος για την επίλυση της δευτεροβάθμιας εξίσωσης με πραγματικούς συντελεστές στο ℝ. Αυτό, βέβαια, δεν σημαίνει απαραίτητα ότι δεν ισχύει ότι κάθε δευτεροβάθμια εξίσωση με πραγματικούς συντελεστές μπορεί να επιλυθεί στο ℝ από μια ειδική (ανά εξίσωση) μέθοδο. Ωστόσο, θα αποδείξω παρακάτω το πιο ισχυρό αποτέλεσμα (-τουλάχιστον στα συνήθη μαθηματικά), ότι δηλαδή μία συγκεκριμένη δευτεροβάθμια εξίσωση με πραγματικούς συντελεστές δεν είναι δυνατό να επιλυθεί στο ℝ (ούτε από μια ειδική μέθοδο) με την προϋπόθεση βέβαια ότι τα συνήθη μαθηματικά έχουν κάποια γνωστή αξία. Όταν μιλάμε για “συνήθη μαθηματικά” εννοούμε το αξιωματικό σύστημα της θεωρίας των συνόλων ZFC, μιας και δεν υπάρχει κάποια συνήθης μαθηματική θεωρία η οποία δεν μπορεί να προσομοιωθεί από το ZFC – γι’ άλλωστε και το ZFC θεωρείται “θεμέλιο” και η πιο γενική μορφή των μαθηματικών. Όταν λέμε ότι “τα συνήθη μαθηματικά έχουν κάποια γνωστή αξία” εννοούμε ότι είναι συνεπή, δηλαδή δεν αποδεικνύουν κάποιον ισχυρισμό και την άρνησή του, δηλαδή μια αντίφαση. Ένα μαθηματικό σύστημα το οποίο αποδεικνύει μια αντίφαση έχει αποδειχτεί ότι μπορεί να αποδείξει οποιονδήποτε ισχυρισμό, κάτι που είναι γνωστό ως “αρχή της έκρηξης”. Ένα τέτοιο σύστημα δεν έχει κάποια γνωστή αξία.
Μια μηχανή Turing είναι ένα μαθηματικό αντικείμενο το οποίο εισήγαγε ο “πατέρας” – κατά κοινή ομολογία – της επιστήμης των υπολογιστών Alan Turing λίγο πριν τα μέσα του προηγούμενου αιώνα, και είναι ισοδύναμο με ένα πρόγραμμα σε μια σύγχρονη γλώσσα προγραμματισμού. “Ισοδύναμο” σημαίνει ότι για κάθε μηχανή Turing υπάρχει ένα πρόγραμμα σε Γλώσσα ΑΕΠΠ, c, java ή οποιαδήποτε άλλη σύγχρονη γλώσσα προγραμματισμού, το οποίο εκτελεί τον ίδιο υπολογισμό, αλλά και αντίστροφα για κάθε πρόγραμμα σε μια σύγχρονη γλώσσα προγραμματισμού, υπάρχει μια μηχανή Turing η οποία εκτελεί τον ίδιο υπολογισμό. Η διαφορά τους είναι ότι η μηχανή Turing είναι πιο απλό (και ένα από τα απλούστερα) υπολογιστικό μοντέλο, με την έννοια ότι η γενική περιγραφή της λειτουργίας μιας μηχανής Turing είναι σχετικά (πολύ) πιο σύντομη. Κάτι τέτοιο ευνοεί φυσικά την μελέτη των ιδιοτήτων του υπολογισμού.
Μια μηχανή Turing εκτελεί έναν υπολογισμό σε διακριτά βήματα, κάτι που σε ένα σύγχρονο προγραμματιστικό περιβάλλον προσομοιάζει με την εκτέλεση ενός προγράμματος βήμα-βήμα στον debugger. Μια άλλη βασική ιδιότητα της μηχανής Turing είναι ότι τερματίζει ή δεν τερματίζει (“κολλάει”). Ισοδύναμα ένα πρόγραμμα σε μια σύγχρονη γλώσσα προγραμματισμού λέμε ότι πέφτει σε “ατέρμονα βρόγχο”, δηλαδή δεν τερματίζει ή κολλάει, ενώ τερματίζει αν δεν πέφτει σε ατέρμονα βρόγχο. Σε κάθε διακριτό βήμα της λειτουργίας της μηχανής Turing μπορεί να αποφασισθεί αν η μηχανή τερματίζει ή όχι (στο συγκεκριμένο βήμα), ενώ το γενικότερο πρόβλημα, δηλαδή αν μια (οποιαδήποτε) μηχανή Turing τερματίζει (σε κάποιο βήμα) ή δεν τερματίζει σε κανένα βήμα έχει αποδειχτεί ότι δεν επιλύεται (τουλάχιστον από μια μηχανή Turing – θα πρέπει να σημειωθεί εδώ ότι η μηχανή Turing – ή ισοδύναμα οποιαδήποτε σύγχρονη γλώσσα προγραμματισμού – είναι το ισχυρότερο υπολογιστικό μοντέλο που έχει ανακαλύψει ο άνθρωπος μέχρι τώρα, με άλλα λόγια σε 4.000 περίπου χρόνια μαθηματικής ιστορίας κανείς δεν έχει παρουσιάσει κάποιον υπολογισμό με χαρτί και μολύβι ή με οποιοδήποτε άλλο μέσο, ο οποίος να μην μπορεί να προσομοιωθεί από μια μηχανή Turing. Η υπόθεση ότι ένα ισχυρότερο από την μηχανή Turing υπολογιστικό μοντέλο δεν υπάρχει, είναι γνωστή ως “θέση Church-Turing”).
Οι Yedidia & Aaronson (2016) κατασκεύασαν την μηχανή Turing Ζ η οποία δεν τερματίζει αν και μόνο αν το ZFC είναι συνεπές, ή ισοδύναμα τερματίζει αν και μόνο αν το ZFC δεν είναι συνεπές. Θεωρείστε τον πραγματικό αριθμό α ο οποίος ορίζεται ως εξής:
Ακέραιο μέρος της δεκαδικής αναπαράστασής του ίσο με το 0 και το νιοστό ψηφίο της δίνεται από την συνάρτηση f(ν), για ν θετικό ακέραιο:

Είναι προφανές ότι:
α = 0 αν και μόνο αν η μηχανή Turing Z δεν τερματίζει (ποτέ)
Ή ισοδύναμα:
α = 0 αν και μόνο αν το ZFC είναι συνεπές (1)
Ή ισοδύναμα:
α ≠ 0 αν και μόνο αν το ZFC είναι ασυνεπές (2)
Θεωρείστε τώρα την ακόλουθη δευτεροβάθμια εξίσωση:
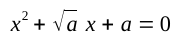
Η διακρίνουσα του τριωνύμου είναι:

Αν κάποιος, λοιπόν, αποδείξει με τα συνήθη μαθηματικά ότι η παραπάνω εξίσωση δεν έχει λύσεις στο ℝ, συνεπάγεται:

Οπότε, από την (2) παίρνουμε ότι το ZFC είναι ασυνεπές, δηλαδή τα συνήθη μαθηματικά είναι άχρηστα.
Αν πάλι αποδείξει με τα συνήθη μαθηματικά ότι η παραπάνω εξίσωση έχει λύσεις στο ℝ, συνεπάγεται:

Οπότε, από από την (1) παίρνουμε ότι το ZFC είναι αποδεδειγμένα συνεπές από το ίδιο το ZFC. Το ZFC, όμως, προσομοιώνει, βέβαια, και την “πρωτοβάθμια αριθμητική Peano”, οπότε από το δεύτερο θεώρημα μη-πληρότητας του Gödel παίρνουμε ότι το ZFC είναι ασυνεπές (εφόσον αποδεικνύει το ίδιο την συνέπειά του)!
Με άλλα λόγια, οποιαδήποτε απόδειξη στα συνήθη μαθηματικά, είτε περί της ύπαρξης, είτε περί της μη-ύπαρξης λύσεων στο ℝ της παραπάνω εξίσωσης τα καθιστά άχρηστα. Άρα, αν δεν είναι άχρηστα, δεν υπάρχει απόδειξη εντός αυτών ούτε ότι η εξίσωση αυτή έχει λύσεις στο ℝ, ούτε ότι δεν έχει. Δηλαδή, η εξίσωση αυτή είναι αδύνατο να επιλυθεί στο ℝ με τα συνήθη μαθηματικά (αν τα τελευταία είναι συνεπή).
